TÌM GIỚI HẠN HÀM SỐ
Có hàm số f(x), để tìm giới hạn khi x tiến về x0 thì dùng hàm Limit với cú pháp Limit[f[x], x->x0]
Nếu cần chỉ rõ x-> x0 từ trái hay phải thì cho thêm tham số:
Direction -> "FromAbove"(tiến đến x0 từ bên phải)Direction -> "FromBelow"(tiến đến x0 từ trái)
Chú ý: \(\infty\) thì dùng hằng số Infinity
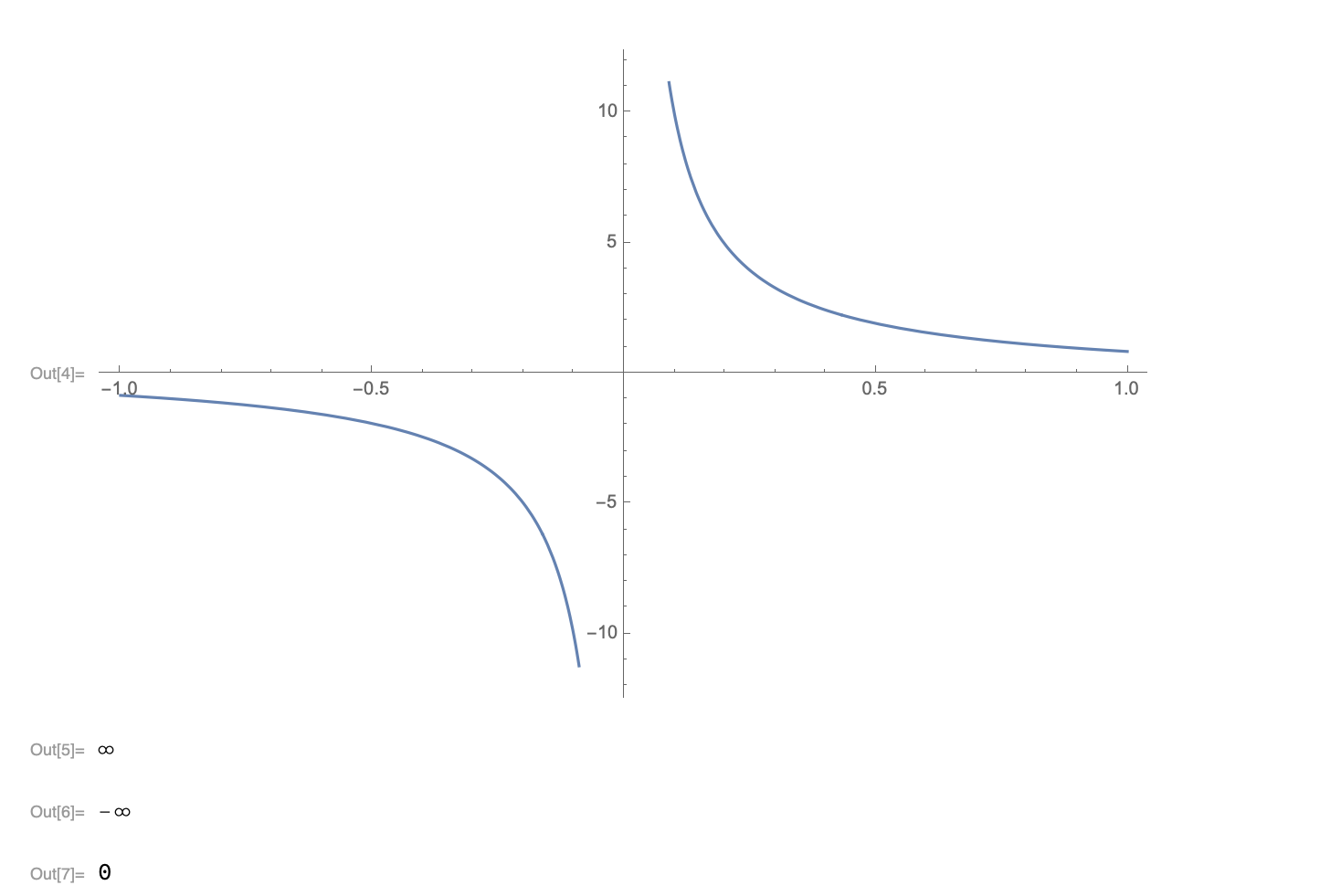
Ví dụ cho hàm số f(x) = \( \frac{\sin (x)}{x^2} \), vẽ đồ thị hàm số, tìm giới hạn thi x -> 0+, x-> 0-, x-> - \(\infty\)
Clear[f];
f[x_] := Sin[x]/x^2
Plot[f[x], {x, -1, 1}]
Limit[f[x], x -> 0, Direction -> "FromAbove"]
Limit[f[x], x -> 0, Direction -> "FromBelow"]
Limit[f[x], x -> -Infinity, Direction -> "FromBelow"]
VÍ DỤ TÌM GIỚI HẠN HÀM SỐ
| Tìm giới hạn | Mathematica | Kết quả |
|---|---|---|
|
lim \(\sqrt{x^2-x}-\sqrt{4 x^2+1}\) Khi x -> \(-\infty \) |
f[x_] := Sqrt[x^2 - x] - Sqrt[4 x^2 + 1] Limit[f[x], x -> -Infinity] |
\(-\infty \) |
|
lim \(\frac{x^2-4}{x^2-3 x+2}\) Khi x -> 2 |
f[x_] := (x^2 - 4) / (x^2 - 3 x + 2) Limit[f[x], x -> 2] |
4 |
|
lim \(x \left(\sqrt{x^2+1}-x\right)\) Khi x -> \(+\infty \) |
f[x_] := x (Sqrt[x^2 + 1] - x) Limit[f[x], x -> +Infinity] |
1/2 |
|
lim \(\frac{\sin ^2\left(\frac{x}{3}\right)}{x^2}\) Khi x -> 0 |
f[x_] := (Sin[x/3])^2 / x^2 Limit[f[x], x -> 0] |
1/9 |

