Khai báo hàm số mới và vẽ đồ thị hàm 2D trong Mathematica

• Khai báo và sử dụng hàm
• Vẽ đồ thị 2D
• Lệnh Plot
• Lệnh GraphicsRow
• Các thiết lập vẽ đồ thị
• Màu nền đồ thị
• Nét vẽ đồ thị
• Thiết lập về hệ trục
• Hàm Table
• Tham số PlotRange
• Tô đồ thị
• Vẽ trong tọa độ cực
• Đồ thị hàm cho bởi tham số
• Vẽ các điểm
• Kết hợp nhiều đồ thị

Xây dụng hàm riêng trong Mathematica

Nếu muốn chuyển biểu thức trở thành một hàm tự định nghĩa, thì cú pháp có thể tham khảo như sau:

myfunction[x_,y_, ...]:=biểu_thức

Trong đó myfunction là tên ham do bạn đặt, tên này để tránh xung đột với các hàm có sẵn của Mathematica nên chọn biết bằng chữ thường. Ký hiệu gạch dưới _ sau mỗi tên tham số là bắt buộc. Để tạo ra các tham số x, x ... thì phải khai báo trong hàm là x_, y_ ..., biểu thức hàm viết sau ký hiệu :=

Nếu hàm số có nhiều biểu thức, thì hàm tạo ra với dạng sau (kết quả hàm trả về là biểu thức cuối biểu_thức_M)

myfunction[x_,y_, ...]:= (a1=biểu_thức_1,
    a1=biểu_thức_2, ... a1=biểu_thức_M)

Ví dụ định nghĩa hàm bậc hai có tên hambachai, biến là x sau đó tính giá trị tại x = 10

Ví dụ hàm nhiều biến z[x_,_y] := x^2 + y^2;

Để tìm miền xác định của một hàm số, dùng hàm FunctionDomain[f, x]

Nếu định nghĩa một hàm có nhiều phần thì bạn cần dùng tới Piecewise[] với tham số là danh sách các phần của hàm kèm điều kiện biến cho phần đó Piecewise[{{biểu-thức-1, điều-kiện-biến1}, {biểu-thức-2, điều-kiện-biến2} ...}]

Ví dụ:

f[x_] := Piecewise[{ {(Sqrt[x + 1] - 1)/x, x > 0}, {2 x^2 + 1, x <= 0}}]

Đó làm hàm: f(x) = \(\begin{array}{cc} \{ & \begin{array}{cc} \frac{\sqrt{x+1}-1}{x} & x>0 \\ 2 x^2+1 & x\leq 0 \\ \end{array} \\ \end{array}\)

Vẽ đồ thị 2D

Lệnh Plot

Để vẽ đồ thị hàm số f, với biến số là x sử dụng hàm Plot[f, {x, xmin, xmax}]. Trong đó xmin, xmax xác định khoảng cần vẽ.

Ví dụ:

Plot[x^2 - 5 x - 10, {x, -10, 15}]

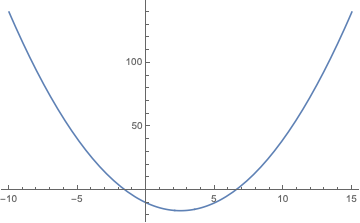
Có thể vẽ nhiều hàm số trên cùng hệ trục, và khoảng cần vẽ Plot[{f1, f2 ..}, {x, xmin, xmax}]

Plot[{x^2 - 5 x - 10, 30 Sin[x]}, {x, -10, 15}]

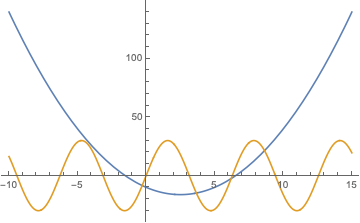
Lệnh GraphicsRow

Mỗi lệnh Plot sẽ xuất ra một hình ảnh đồ thị trên một dòng kết quả. Nếu muốn các ảnh này cùng nằm trên một dòng thì dùng thêm hàm GraphicsRow[{...}], tham số là danh sách các lệnh Plot

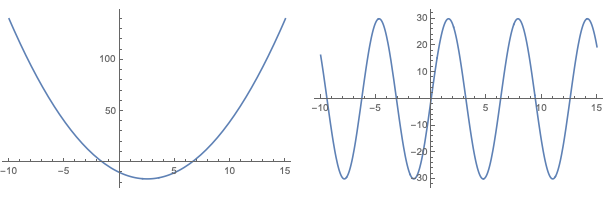
GraphicsRow[
    {Plot[x^2 - 5 x - 10, {x, -10, 15}], Plot[ 30 Sin[x], {x, -10, 15}]} ]

Các thiết lập vẽ đồ thị

Có rất nhiều tham số thiết lập để vẽ đồ thị, lệnh sau hiện thị các tham số đó

Partition[Options[Plot] , 3] // TableForm

Trong đó:

• Options[Plot] để lấy danh sách các thiết lập vẽ đồ thị
• Partition[list,n] nhóm một danh sách thành nhóm các danh sách n phần tử
• TableForm in dữ liệu với định dạng bảng

Từ các tên các tham số đó muốn tùy chỉnh cách thể hiện đồ thì thì đưa vào hàm Plot sau sau các tham số đã biết cách nhau bởi dấu ,

Nền đồ thị

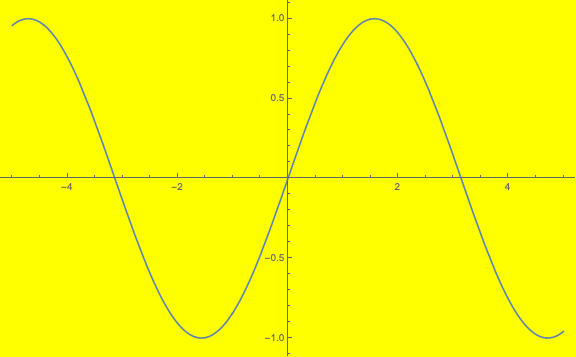
Ví dụ đặt lại nền cho đồ thị thì dùng tham số Background, nếu đặt màu nền vàng thì thêm Background->Yellow vào tham số:

Plot[ Sin[x], {x, -5, 5},   Background -> Yellow]

Thiết lập đường vẽ đồ thị

Có thể thiết lặp đường vẽ bằng cách gộp những thuộc tính tính của đường với hàm Directive[g1, g2 ...] trong đó g1, g2, ... là các thuộc tính đường vẽ, nó có thể là:

• Màu của đường cần vẽ, chỉ ra bởi tên màu như Red, Green, Blue, Black, White, Gray, Cyan, Magenta, Yellow, Brown, Orange, Pink, Purple ... hoặc màu trộn bằng hàm RGBColor[red, green, black, opacity]
• Độ dày của đường xác định bởi hàm Thickness[r] với r là là tỷ số điểm điểm vẽ và chiều ngang cần vẽ, ví dụ Thickness[1/100] độ dày bằng 1/100 của chiều rộng đồ thị. Hoặc dùng hằng số Thin (mỏng), Thick (dày)
• Kiểu nét: Dashed (nét đứt), Dotted (điểm), DotDashed (chấm - gạch), nếu dùng Dashing[r] thì có thể thiết lập tùy chọn độ dài nét đứt với r là hệ số chiều dài và độ rộng đồ thị,

Kích thước đồ thị vẽ có thể chọn với tham số ImageSize với thiết lập ->bằng các giá trị như Tiny, Small, Medium. Medium, Large, Full

Ví dụ:

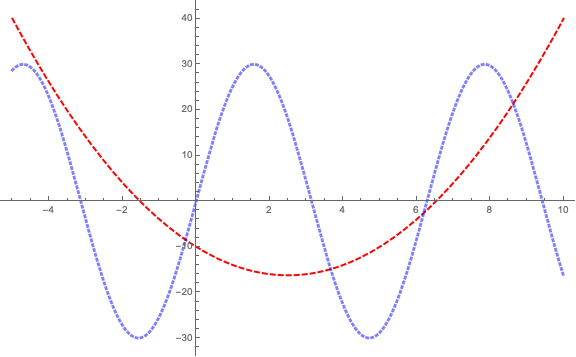
Plot[
 { x^2 - 5 x - 10, 30 Sin[x]}, {x, -5, 10},
 PlotStyle ->
  {
     Directive[Red,  Dashed, Thick],
     Directive[RGBColor[0, 0, 1, .5], Thickness[1/200], Dotted]
   },
 ImageSize -> Large
 ]

Thiết lập về hệ trục tọa độ

LabelStyle cũng được gán bằng Directive[g1, g2, ...] để định dạng nhãn trên hệ trục tọa độ, các thiết lập g1, g2 ... có thể quan tâm như:

• Cơ chữ Tiny, Small, Medium. Medium, Large, Full
• Màu chữ tên màu ở trên (Green, Yellow ...
• Bold (đậm), Italic (nghiêng), Underlined (gạch chân) ...

Tham số Axes để bật tắt một trục nào đó ví dụ Axes -> False (hoặc Axes -> {false, false} để tắt cả 2 trục tọa độ, Axes -> {True, False} chỉ vẽ trục hoành ...

AxesLabel-> {"nhãn X", "nhãn Y"} để thay đổi tên trục

AspectRatio để thiết lập hệ số giữa tung độ và hoành độ, mặc định nó vẽ theo tỷ lệ vào 1 / GoldenRatio với GoldenRatio = 1.61803, nếu muốn thiết lập tỷ lệ 1:1 giữa tung độ và hoành độ thì AspectRatio->Automatic

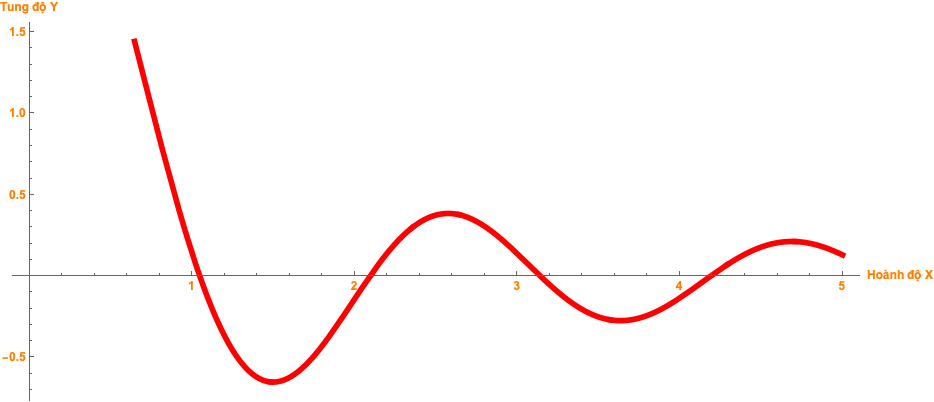
Plot[
      Sin[3 x]/x, {x, 0, 5},
      PlotStyle -> Directive[Red, Thickness[1/150]],
      ImageSize -> Full,
      LabelStyle -> Directive[Orange, Bold, Medium],
      AxesLabel -> {"Hoành độ X", "Tung độ Y"},
      AspectRatio -> Automatic
 ]

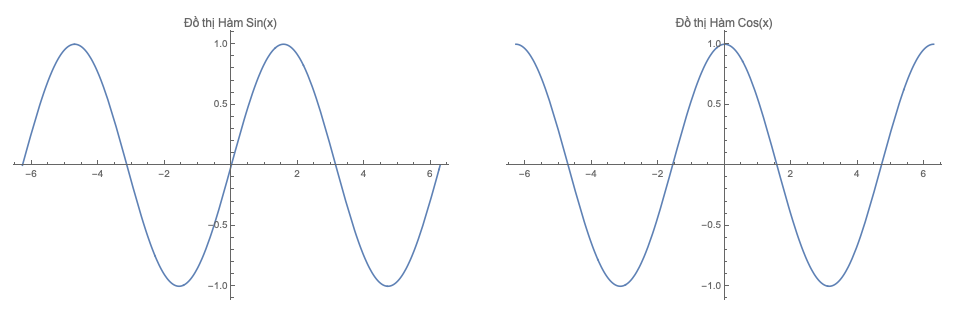
Để đặt tên đồ thị, sử dụng thiết lập PlotLabel->"tên đồ thị"

GraphicsRow[{
  Plot[
   Sin[ x], {x, -2 Pi, 2 Pi},
   PlotLabel -> "Đồ thị Hàm Sin(x)"
   ],
  Plot[
   Cos[ x], {x, -2 Pi, 2 Pi},
   PlotLabel -> "Đồ thị Hàm Cos(x)"
   ]
  }]

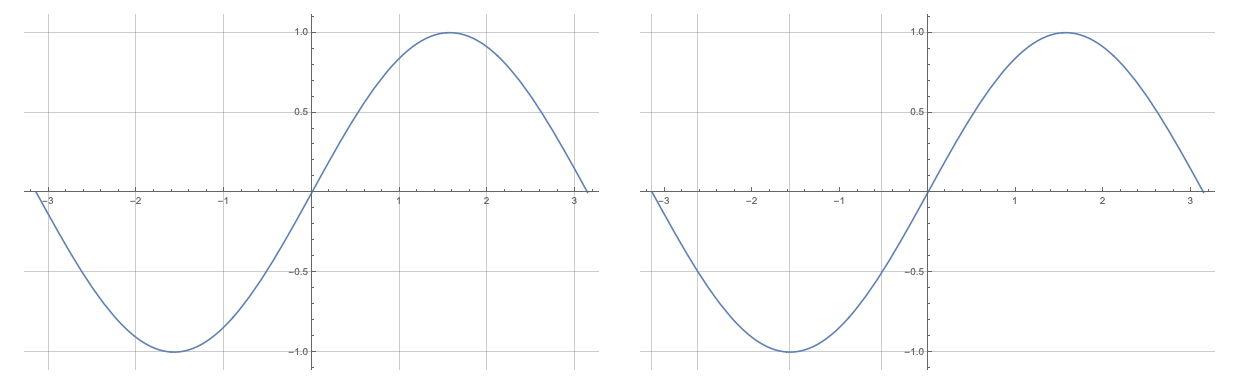
Để kẻ lưới đồ thị, sử dụng tham số GridLines nếu GridLines -> Automatic kẻ lưới đơn vị, nếu muốn kẻ theo lưới x, y chỉ định dùng GridLines -> {{x1, x2, ...}, {y1, y2, ...}}

GraphicsRow[{
  Plot[
    Sin[x], {x, - Pi,  Pi},
    GridLines -> Automatic,
    ImageSize -> Large],

  Plot[
    Sin[x], {x, - Pi,  Pi},
    GridLines -> {{-Pi, - 5 Pi / 6, -Pi/2, -Pi /6 }, {-1, -0.5, 0.5,
      1}},
    ImageSize -> Large]
  }]

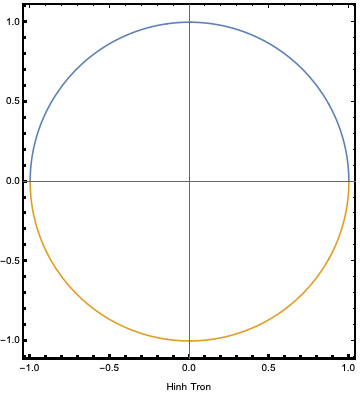
Muốn vẽ với khung vuông đồ thị thì các tham số Frame, FrameLabel, FrameStyle được sử dụng

Plot[
      {Sqrt[1 - x^2], -Sqrt[1 - x^2]}, {x, -1, 1},
     Frame -> True,
     FrameLabel -> "Hinh Tron",
     FrameStyle -> Directive[Black, Thick],
      ImageSize -> Medium,
     AspectRatio -> Automatic
 ]

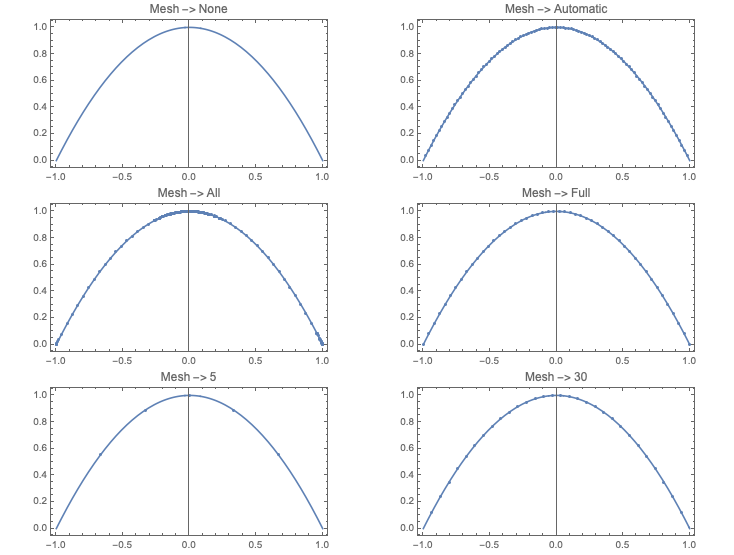
Tham số Mesh cho phép nhấn mạnh một số điểm trên đồ thị với các giá trị như: Mesh -> All nhấn mạnh tất các các điểm mẫu, Mesh -> Full các điểm cách nhau một khoảng nhất định, Mesh -> n chia ra thành n điểm ...

Ví dụ:

GraphicsGrid[
     Partition[
          Table[
               Plot[1 - x^2, {x, -1, 1},
                    Mesh -> m,
                    ImageSize -> Medium,
                    Frame -> True,
                    AspectRatio -> Automatic,
                    PlotLabel -> "Mesh -> " <> ToString[m]],

                {m, {None, Automatic, All, Full, 5, 30}}],
          2],
     Spacings -> 1
]

Trong công thức vẽ đồ thị phía trên để ý một số hàm sau:

Hàm Table

Table[expr, {i, n}] hàm sinh ra một danh sách (List) từ biểu thức với i chạy từ 1 tới n. Nếu muốn i là từng phần tử của một danh sách {i1, i2 ...} thì viết Table[expr, {i, {i1, i2 ...}}]

GraphicsGrid để xuất một lưới các ảnh đồ thị. Dữ liệu là một nhóm các dòng danh sách, ở ví dụ trên dữ liệu sinh ra bởi Partition (biểu diễn một danh sách thành nhiều danh sách nhỏ với số lượng phần tử chỉ ra).

<> là toán tử để nối chuỗi

Tham số PlotRange

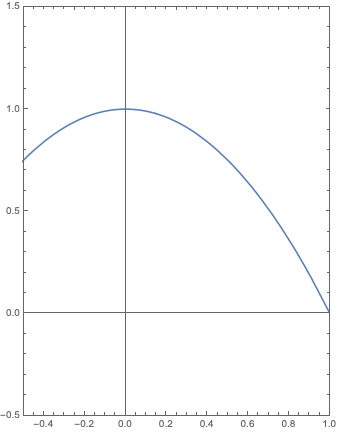
Để thiết lập hình chữ nhật giới hạn đồ thị sẽ vẽ ra ví dụ trục x từ xmin đến xmax, trục y từ ymin đến ymax thì dùng tham số PlotRang với cú pháp PlotRange-> {{xmin, xmax}, {ymin, ymax}}

Plot[
     1 - x^2, {x, -10, 10},
     ImageSize -> Medium,
     Frame -> True,
     PlotRange -> {{-0.5, 1}, {-0.5, 1.5}},
     AspectRatio -> Automatic]

Tô đồ thị

Để thiết lập tô đặc đồ thị có 2 tham số đó là Filling thiết lập cách giới hạn vùng tô và FillingStyle gán bằng Directive thiết lập kiểu tô (màu, độ trong ...)

Filling có thế nhận các giá trị như:

• Filling -> Top không gian giới hạn bởi đường cong và đường ngang y giới hạn trên
• Filling -> Bottom không gian giới hạn bởi đường cong và đường ngang y giới hạn dưới
• Filling -> Axis không gian giới hạn bởi đường cong trục tọa độ
• Filling -> Yvalue không gian giới hạn bởi đường cong và đường ngang giá trị Yvalue

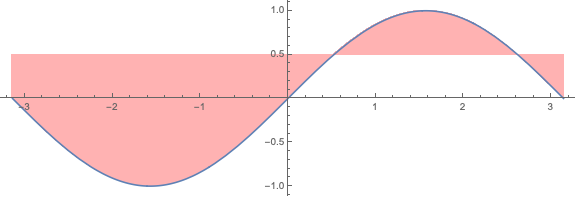
Plot[
 Sin[x], {x, - Pi, Pi},
 ImageSize -> Large,
 Frame -> False,
 AspectRatio -> Automatic,
 Filling -> 0.5,
 FillingStyle -> Directive[Red, Opacity[0.3]]]

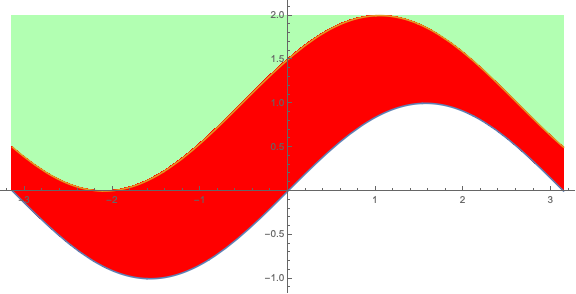
Tham số Filling cũng có thể chỉ ra vùng tô giới hạn bởi 2 hay nhiều đường cong. Ví dụ nếu có 2 đường cong thì tô vùng giới hạn bởi hai đường cong sẽ thiết lập là Filling -> {1 -> {2}}, cũng có thể thêm thiết lập màu vào vùng tô này Filling -> {1 -> {{2}, Red}} có thể thay Red bằng Directive

Plot[
 {Sin[x], Sin[x + Pi/6] + 1}, {x, - Pi, Pi},
 ImageSize -> Large,
 Frame -> False,
 AspectRatio -> Automatic,
 Filling ->  {
                      1 -> {{2}, Red},
                      2 -> {Top, Directive[Green, Opacity[0.3]]}
   }
 ]

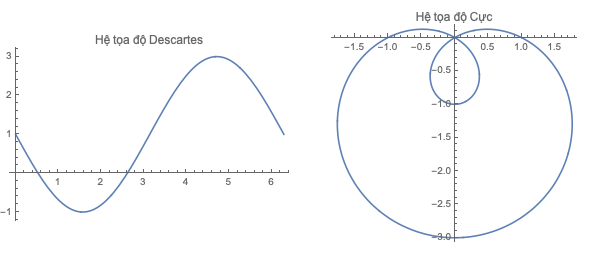
Vẽ đồ thị trong tọa độ cực với Mathematica

Để vẽ hàm số trong hệ tọa độ cực dùng hàm PolarPlot với các tham số tương tự Plot

f = 1 - 2 Sin[theta];
GraphicsRow[{
  Plot[f, {theta, 0, 2 Pi}, PlotLabel -> "Hệ tọa độ Descartes"],
  PolarPlot[f, {theta, 0, 2 Pi}, PlotLabel -> "Hệ tọa độ Cực"]
  }]

Vẽ đồ thị hàm cho bởi tham số

Hàm số bình thường vẫn quen có dạng y = f(x) tuy nhiên có những hàm thì y và x lại xác định qua một biến số khác ví dụ x = x(t); y - y(t); đó là hàm tham số, để vẽ hàm cho bởi tham số dùng hàm Mathematica ParametricPlot với các thiết lập giống như Plot.

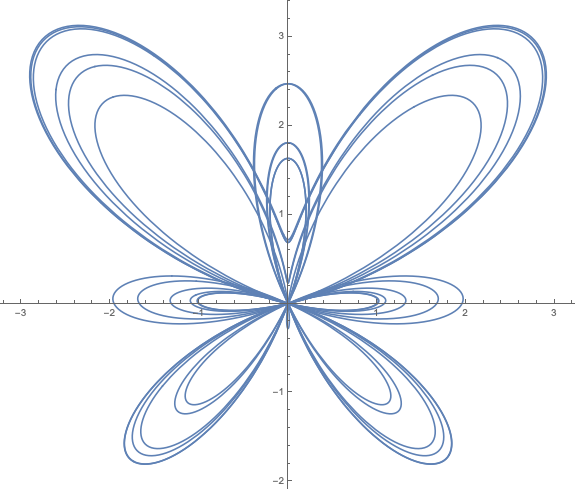
Ví dụ vẽ đường cong con bướm Butterfly curve (transcendental) , đường cong này cho bởi hàm tham số

x = Sin[t] (E ^ Cos[t] - 2 Cos[4 t] - Sin[t /12]^5)
y = Cos[t] (E ^ Cos[t] - 2 Cos[4 t] - Sin[t /12]^5)
ParametricPlot[{x, y}, {t, 0, 12 Pi}, ImageSize -> Large]

Vẽ các điểm

Để vẽ các điểm sử dụng hàm ListPlot[data], trong đó data là danh sách các điểm, sau nó có các thiết lập tương tự Plot

Khi danh sách cho bởi các giá trị dạng data = {y1, y2, y3 ...} thì nó là tung tộ của các hoành độ tương đối tương ứng x1 = 1, x2 = 2 ...

Ví dụ: Một số điểm thuộc hàm Sin(x) - data = Table[Sin[x] // N, {x, 0, 2 Pi, 1}]

data = {0.0, 0.841471, 0.909297, 0.14112, -0.756802, -0.958924, -0.279415}
ListPlot[data, ImageSize -> 500]

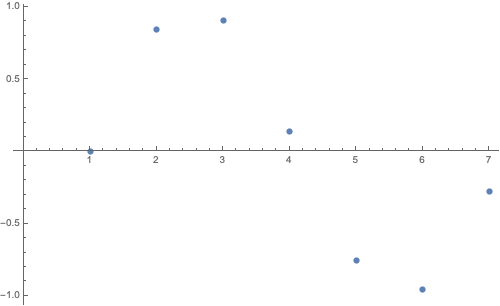
Nếu muốn chỉ ra chính xác tọa độ các điểm, dữ liệu data nhập vào dạng: data = { {x1, y1}, {x2, y2} ...}

Ví dụ các điểm thuộc hình Sin ở trên data = Table[{x, Sin[x]} // N, {x, 0, 2 Pi, 1}]

data = {{0., 0.}, {1., 0.841471}, {2., 0.909297}, {3.,0.14112}, {4., -0.756802}, {5., -0.958924}, {6., -0.279415}}
ListPlot[data, ImageSize -> 500]

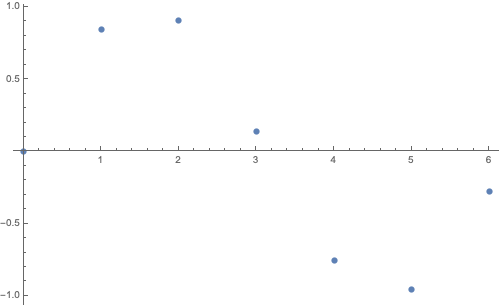
Ngoài các tham số thiết lập giống như Plot, gõ lệnh sau để xem một số tham số thiết lập thêm cho LIstPlot:

Options[ListPlot], Options[Plot]

{DataRange -> Automatic, InterpolationOrder -> None, Joined -> False,
 LabelingFunction -> Automatic, MaxPlotPoints -> \[Infinity],
 PlotLayout -> "Overlaid", PlotMarkers -> None,
 PlotRange -> Automatic}

InterpolationOrder để thiết lập các điểm vẽ tính toán lại bằng cách nội suy.

• InterpolationOrder->1 nối suy bậc nhất (nối thẳng các điểm với nhau)
• InterpolationOrder->2 nội suy đường cong bậc II
• InterpolationOrder->3 nội suy đường cong bậc III ...

Joined->True để thiết lập đồ thị nối qua các điểm

data = Table[{x, Sin[x]} // N, {x, 0, 2 Pi, Pi / 4}]
GraphicsRow[{
  ListPlot[data, ImageSize -> 500, Joined -> True, InterpolationOrder -> 1],
  ListPlot[data, ImageSize -> 500, Joined -> True, InterpolationOrder -> 2]
}]

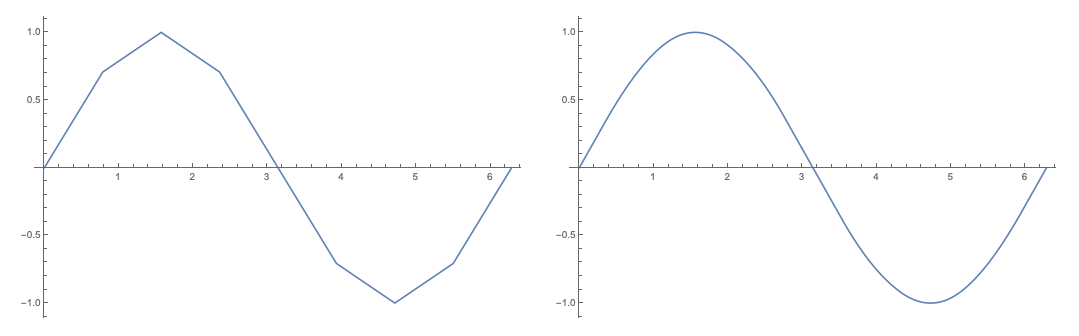
Bạn có thể thiết lập cỡ điểm vẽ và màu sắc với thiết lập PlotStyle

data = Table[{x, Sin[x]} // N, {x, 0, 2 Pi, Pi / 4}]
ListPlot[data, ImageSize -> 500, PlotStyle -> {AbsolutePointSize[10], Red}]

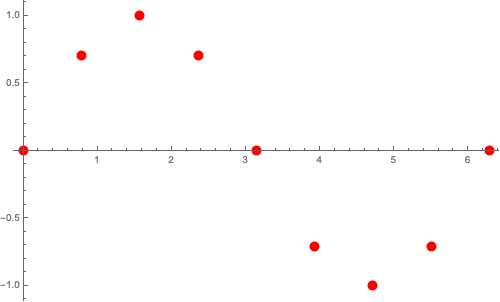
Kết hợp nhiều đồ thị

Khi vẽ các đồ thị bằng Plot, ListPlot ... bạn có thể kết hợp chúng lại trên một hệ trục với hàm Show[Plot[], ListPlot[], ...], trong đó đồ thị đầu tiên làm chuẩn để các đồ thị khác lồng vào

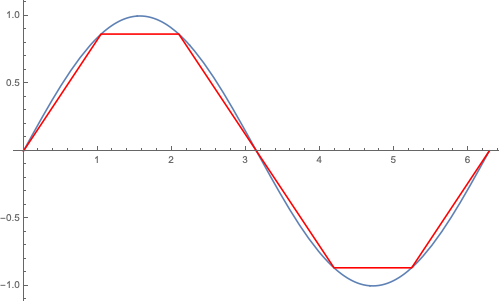
data = Table[{x, Sin[x]} // N, {x, 0, 2 Pi, Pi / 3}]
Show[
   Plot[Sin[x], {x, 0, 2 Pi}],
   ListPlot[data, ImageSize -> 500, Joined -> True, PlotStyle -> {Red}]
 ]

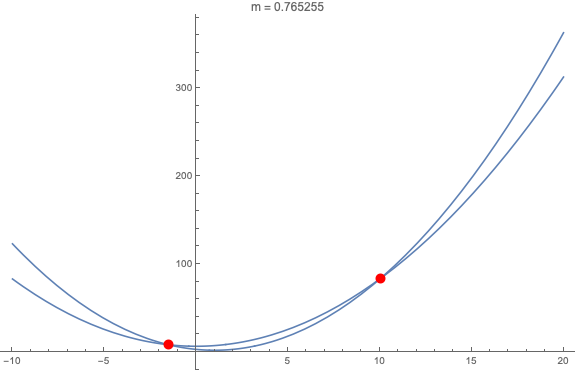
Ví dụ: tìm giao điểm của y = $3-2x+x^2$ và của y = $5+2m+m{x}^2$, vẽ đồ thị và đánh dấu giao điểm của 2 đường đó.

Clear[f1, f2, x, m, x1, x2];
f1[x_] := x^2 - 2 x + 3
f2[x_, m_] := m x ^2 + 2 m + 5

ketqua = Solve[f1[x] == f2[x, m] , {x}, Reals]
x1 = x /. ketqua[[1]] // Normal
x2 = x /. ketqua[[2]] // Normal

data = {{x1, f1[x1]}, {x2, f1[x2]}}

Manipulate[
 Show[
      Plot[f1[x], {x, -10, 20 }],
      Plot[f2[x, mm], {x, -10, 20 }],
      ListPlot[data //. m -> mm,
      PlotStyle -> {AbsolutePointSize[10], Red}],

      ImageSize -> Large,
      PlotLabel -> "m = " <> ToString[mm]
  ]
 , {mm, -Sqrt[3/2], Sqrt[3/2], 0.01}]