Hàm toán học sơ cấp và nhập số liệu Mathematica

Trong Mathematica cung cấp sẵn rất nhiều các hàm (lệnh) toán học xây dựng sẵn, từ các hàm sơ cấp đến các hàm phức tạp. Các hàm này có cấu trúc chung gồm Tên (luôn bắt đầu bằng chữ hoa như Power, Sin, Plot ...), liền sau đó là cặp ngoặc vuông [], trong cặp ngoặc vuông này là các đối số (giá trị, biến, biểu thức hay hàm nào đó) phân cách bởi dấu ,

Ví dụ hàm Sqrt dùng để tính căn bậc 2, nó có một đối số:

 In[9]:= Sqrt[2] // N
Out[9]:= 1.41421

Hàm Power để tính lũy thừa thì lại có hai đối số. Đối số thứ nhất là cơ số và đối số thứ 2 là số mũ

 In[9]:= Power[2, 0.345]
Out[9]:= 1.27015

Một số hàm toán học sơ cấp trong Mathematica

Dưới đây là một số hàm thông dụng:

Sqrt[x]	Căn bậc 2 của x: $\sqrt{x}$, hoặc có thể viết x ^ (1/2)
Exp[x]	Tính e mũ x : $e^x$ hoặc bạn có thể viết E ^ x
Log[x]	Logarit tự nhiên của x
Log[a, x]	Logarit cơ số a của x :
Six[x]	Hàm lượng giác Sin(x), tương tự có Cos[x], Tan[x], ArcSin[x], ArcCos[x], ArcTan[x]
n!	Giai thừa của n
Abs[x]	Trị tuyệt đối của x
Round[x]	Làm tròn
Mod[a, b]	Lấy phần nguyên của phép chia a / b
Random[]	Phát sinh số ngẫu nhiên trong khoảng [0 - 1]
Max[x, y, ...]	Tìm số lớn nhất trong các số x, y ...
Min[x, y, ...]	Tìm số nhỏ nhất trong các số x, y ...
FactorInteger[n]	Tìm các số nguyên tố của n (phân tích số nguyên n thành tích các số nguyên tố).

Bạn có thể chỉ định biểu-thức là đối số của hàm Function bằng cách viết:
biểu-thức //Function
Thay cho cách viết thông thường
Function[biểu-thức]

Trong Mathematica cũng định nghĩa sẵn các hằng số gồm:

Pi	$\pi$ ≃ 3.14159
E	e ≃ 2.71828 (thường xuất kết quả với ký hiệu e)
Degree	Độ = Pi / 180
I	Đơn vị ảo (xuất với ký hiệu i), với i = $\sqrt{-1}$
Infinity	$\infty$

Ví dụ:

 In[9]:= Sin[30 Degree] // N
Out[9]:= 0.5

Tùy chọn độ chính xác kết quả tính

Trong phần trước, nếu muốn lấy kết quả dạng số của biểu thức thì thêm vào sau biểu thức đó ký hiệu //N

Ngoài ra bạn cũng có thể dùng hàm có tên N để chứa biểu thức để có kết quả tương tự.

 In[9]:= N[Sqrt[2]]
Out[9]:= 1.41421

Nếu muốn kết quả có độ chính xác với n chữ số sau dấu chấm thì viết N[biểu-thức, n], ví dụ kết quả chính xác với 20 chữ số dấu chấm động

 In[9]:= N[Sqrt[2], 20]
Out[9]:= 1.4142135623730950488

Số phức

Cung cấp đơn vị ảo I nên ta có thể dễ dàng biểu diễn số phức trong Mathematica

Ví dụ số phức a + bi (trong đó a là phần thực, b là phần ảo và i là đơn vị ảo) thì viết là a + b I

 In[9]:= 2 + 3 I
Out[9]:= $2+3i$

Một vài hàm trên số phức

Re[z]	Lấy phần thực của số phức z
Im[z]	Lấy phần ảo của số phức z
Conjugate[z]	Tìm số phức liên hợp z
Abs[z]	Tính module của z (trị tuyệt đối)
Arg[z]	Tính góc Argumen của z

Nhập liệu các biểu thức trong Mathematica

Ngoài cách sử dụng các dòng chữ như ở các phần trước, bạn có thể nhập biểu thức và ký hiệu bằng cách bấm chọn các bảng công cụ gọi là các palette, nếu bảng này chưa có bạn chọn ở menu Palettes > Basic Math

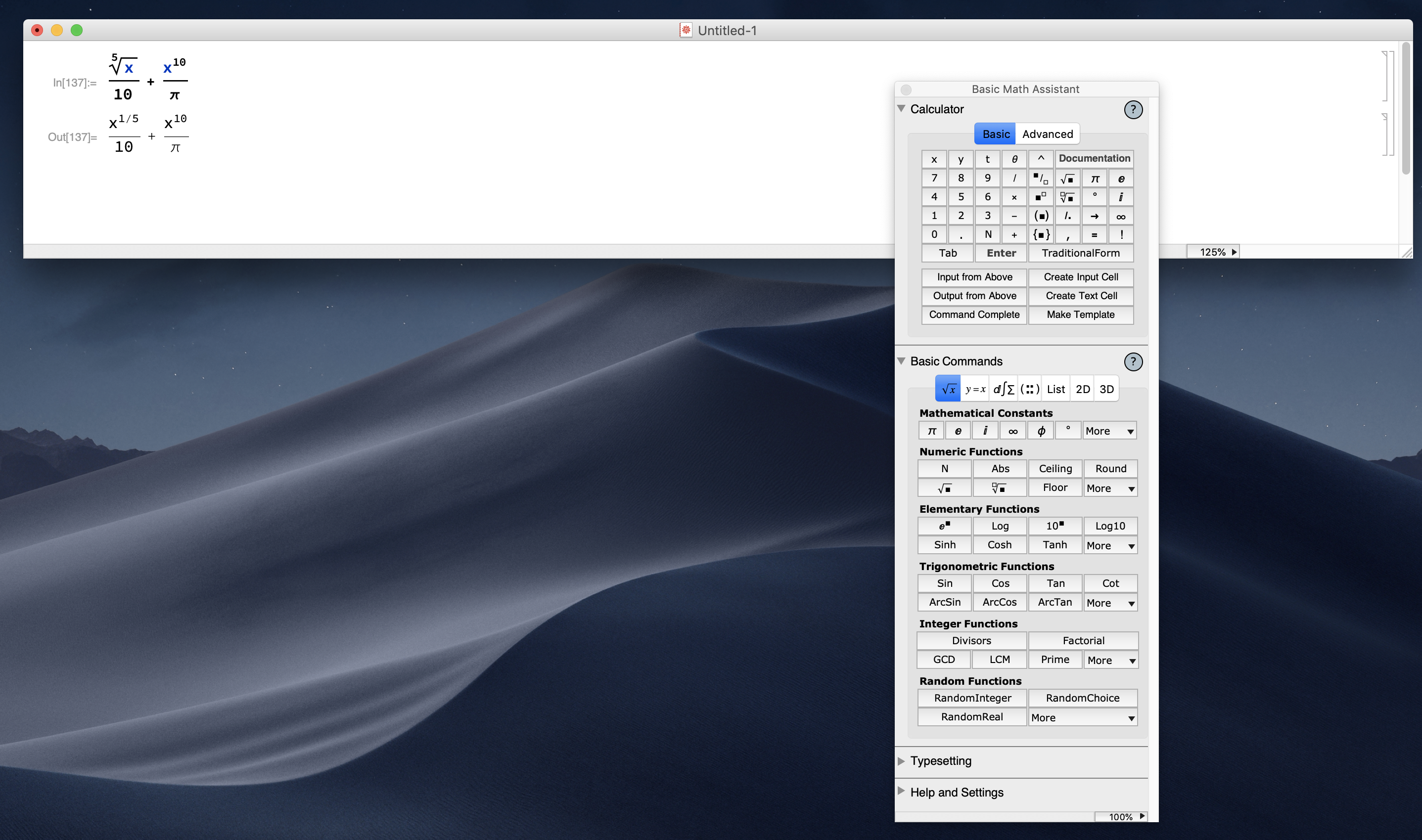
Ngoài ra bạn gõ từ bàn phím để chọn nhanh các ký hiệu như sau

CTRL + /	$\frac{}{}$ phân số
ESC + p	$\pi$
CTRL + 2	$\sqrt{}$ căn bậc 2
CTRL + 2, CTRL + 5	$\sqrt[]{}$ căn bậc n
CTRL + 6	${}^{}$ lũy thừa (số mũ)
ESC + inf	$\infty$
ESC + ee	hằng số e
ESC + ii	đơn vị ảo i
ESC + deg	độ $°$